Solving A System Of Second Order Differential Equations In Matlab
Solving a system of second order differential equations in matlab. Finding the global maxima of stalagmite function using genetic algorithm. Here the first and second equations have second-order derivatives of x t and y t. Solve Differential Equation with Condition.
Solving First Order Differential Equations with ode45 The MATLAB commands ode 23 and ode 45 are functions for the numerical solution of ordinary differential equations. To solve a system of differential equations see Solve a System of Differential Equations. This example shows you how to convert a second-order differential equation into a system of differential equations that can be solved using the numerical solver ode45 of MATLAB.
The key to this is to break down a second order into two first order ODEs. Solving Second Order Differential Equations in Matlab 41 Reducing a higher order DE to a system Method of Undetermined Coefficients - Part 2 Solving second order differential equation using operator D Nonhomogeneous 2nd-order differential equations. To solve a system of differential equations see Solve a System of Differential Equations.
Solve Differential Equation with Condition. Reduce the system to a first-order system by using reduceDifferentialOrder. This example shows you how to convert a second-order differential equation into a system of differential equations that can be solved using the numerical solver ode45 of MATLAB.
Example 1 - A Generic ODE Consider the following ODE. First represent u and v by using syms to create the symbolic functions ut and vt. Du dt 3 u 4 v dv dt - 4 u 3 v.
Solving systems of first-order ODEs. Solve a system of equations to return the solutions in a structure array. How to solve coupled differential equations dependend on data stored in arrays 1 Solving System of Second Order Ordinary Differential Equation in Matlab.
The solve function returns a structure when you specify a single output argument and multiple outputs exist. Nonlinear Differential Equation with Initial Condition.
They use the Runge-Kutta method for the solution of differential equations.
I wish to get the solution where my output is xyz position vs. Syms u v eqns 2u v 0 u - v 1. Solve Differential Equation with Condition. To simulate this system create a function osc containing the equations. To solve a system of differential equations see Solve a System of Differential Equations. Solve a system of equations to return the solutions in a structure array. Springs and Anti roll bar selection for a Sedan and plotting the bump oscillation profile. A typical approach to solving higher-order ordinary differential equations is to convert them to systems of first-order differential equations and then solve those systems. Reduce the system to a first-order system by using reduceDifferentialOrder.
Preallocate space in a column vector and. Thus the differential order is 2. We can solve a second order differential equation of the type. Preallocate space in a column vector and. Y 1 00 y 2 01 van der Pol equations in relaxation oscillation. Solve Differential Equation with Condition. Quasi 1D simulation of a Subsonic-Supersonic Nozzle.





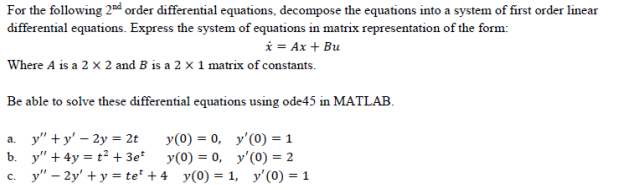







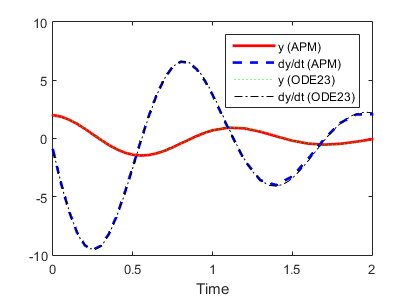

















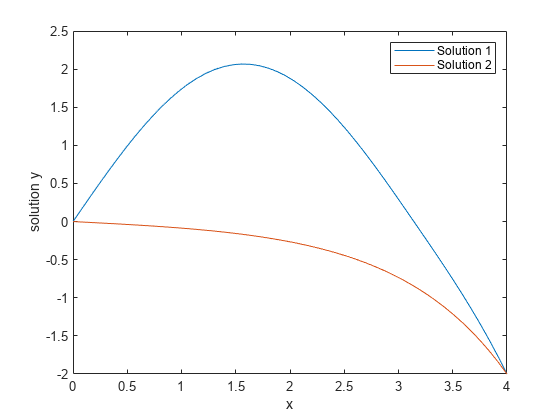

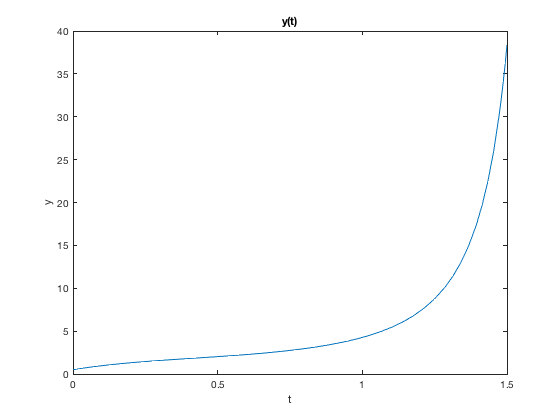











Post a Comment for "Solving A System Of Second Order Differential Equations In Matlab"